| Water Simulation (Win32) | 2006-9-9, ZIP File 234kB |
I became interested in the complicated reflection patterns of rippling water, and wanted to see if I could come up with a reasonably good approximation of the effect that would run in realtime. This demonstration program was the result. Unfortunately, the source code for this program has been lost.
| Water Simulation (Win32) | 2006-9-9, ZIP File 234kB |
I started by building a 3D model of the pool in my backyard. It has the same basic features as the real pool: a diving board, ladder, stairs with a railing, et cetera. I also borrowed a fractal tree from a previous demonstration.
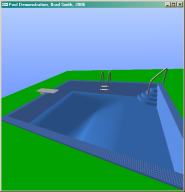


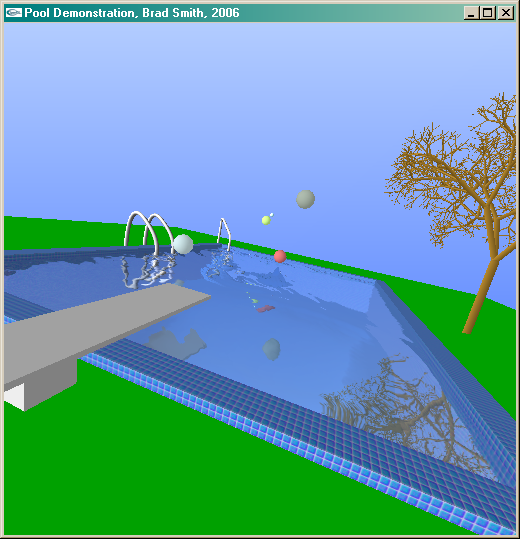
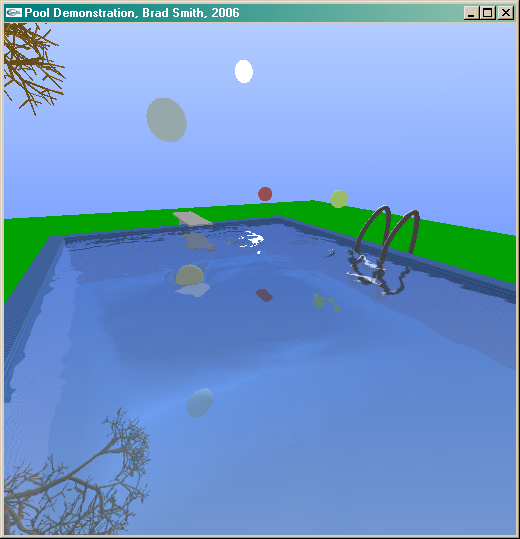
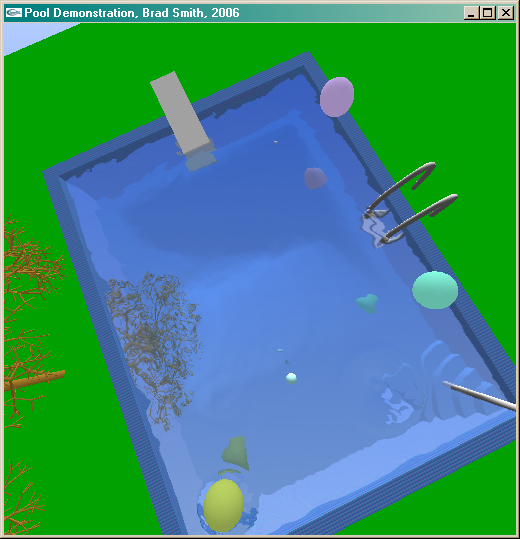
The next step was to create a water surface. This was done as a grid heightmap that fit inside the pool. To simulate the vertical wave motion, I treated each wave as a spring that (at each frame of animation) recieves an acceleration toward the base water height. This creates a sinusoidal oscillation (remember that the second derivative of sin(x) is -sin(x), thus acceleration equal to the inverse of position generates a sine wave). This is combined with an acceleration toward the average of the surrounding four points, allowing the wave to travel outwards horizontally as well.
A hexagonal packing of the surface was also tested, but this offered very little improvement of the wave shape at the cost of 3/2 as much memory access, so the square grid was preferred instead.
Once the heightmap is created, normals to the surface are found by using a simple gradient. I added bouncing balls to the demonstration to create a source of waves.
With the waves in place, I wanted the water to both reflect the scene above, and show through the scene below (with refraction from the ripples). My solution was to make two dynamic texture maps, one for the reflections, and one for the refractions. This gives the whole operation three rendering passes per frame.
The first texture contains the part of the scene below the baseline water level. This is accomplished by using a custom clipping plane to cut off all parts of the scene above the water, and simply rendering that. The second texture uses the same clipping plane, but the entire scene is flipped upside down, thus generating the reflected view.
With these two textures ready, a vertex shader is used to determine the on-screen location of each water vertex. This location is used to look up the corresponding part of the two textures. To create the ripple effect, these texture coordinates are each offset by some amount determined by the water's surface normal. In the fragment shader these two textures are simply summed. The effect, I think, is quite nice.
In this demonstration, the percentage of reflected versus refracted light is somewhat high. I did this to emphasize the reflective effect, but the vertex shader could easily be modified to make the balance proportional to the angle the water is viewed from. In this program, however, instead of doing such a calculation in the shader, I "pre-blended" them by reducing the light for the two texture renderings by half. This was primarily a speed optimization, but also allowed me to create a "bright sun" effect, by having the sun's reflection not affected by the lower light.
The under-water refraction could be made more realistic by determining the average change in refractive angle of the scene, and using a vertex shader to warp the under-water vertex coordinates (in the under-water rendering pass) to approximately match the refractive effect of the water. I did not implement this in this demonstration, because I considered the ripple-refraction effect to be convincing enough.