Arcball
When viewing three dimensional objects there are many different ways to
allow a user to choose a viewpoint, but the method I have found to be the most
intuitive is the arcball. (For examples of many different methods, visit
Chris Rorden's page.)
The basic principle of the arcball is this: create a sphere around the object,
and allow the user to click a point on the sphere and drag that point to
a different location on the screen, having the object rotate to follow it.
The following ZIP file contains C++ source code implementing an arcball
in OpenGL, the mechanics of which will be explained on this page.
It also includes the example Earth program which I used to
demonstrate its function, and source code for a small sample program using GLUT.
This arcball source code is free to use and modify for any purpose,
with no restrictions of copyright or license.
If you have any comments or questions, please e-mail them to me. My
address appears at the bottom of this webpage.
|
Finding the Mouse Position
The first step in finding the mouse position is to aquire the
viewing transformation matrices from OpenGL. I recommend setting up
your view using just the PROJECTION matrix
and then acquiring it directly from OpenGL with glGetDoublev.
(I'm assuming that the MODELVIEW matrix is identity for
the viewer, so I leave it as is.)
GLdouble projection_matrix[16] = {1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1};
GLdouble modelview_matrix[16] = {1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1};
int viewport_matrix[4] = {0,0,640,480};
glGetDoublev(GL_PROJECTION_MATRIX,projection_matrix);
glGetIntegerv(GL_VIEWPORT,viewport_matrix);
Once these matrices have been acquired and stored for future use, we
can use them to handle mouse input. Knowing the mouse coordinates
mouse_x, and mouse_y, we can use gluUnProject
to acquire the coordinates of a point in the scene that is under the mouse.
Note, though, that OpenGL counts from the bottom left corner whereas
most windows interfaces count from the top left, so you may need to
invert your mouse_y coordinates.
(e.g. mouse_y = (window_height - 1) - mouse_y;)
GLdouble x,y,z;
gluUnProject(mouse_x, mouse_y, 0.0,
modelview_matrix,
projection_matrix,
viewport_matrix,
&x, &y, &z);
Once a point in the scene has been found, it is a matter of creating a
ray from the camera location to that point, then finding the intersection
of that ray with your sphere. Your ray is the set of points E + t*(P - E),
where E is the eye location, P is the point in the scene, and
t is a variable parameter. Similarly, your sphere is the set of
points S where S2 = r2, r being the radius.
If S = E + t*(P - E), then the point exists both on the sphere
and the ray, so we can make a substitution to determine that
(E + t*(P - E))2 = r2. I will leave the algebra up to
you, but the gist of it is that you know the
vectors
E, P, and the
scalar
r, so t can be found by plugging them in. You'll get a
quadratic
equation which gives from 0 to 2 solutions. If there's no solution, your
ray does not intersect the sphere (there are many ways to deal with
this, I will not go into them here), and if there are two, you should
pick the one that gives the point closest to the eye.
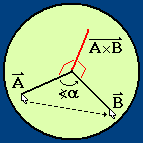
A diagram of the basic principle of the arcball's rotation.
Determining the Arcball's Rotation
If you click and drag one point on the sphere to another location,
the question that must be answered is "how do I rotate the sphere to
move the original point to the new location?" The perhaps unexpected
answer is that there are really an infinite number of ways to do it.
Imagine putting your finger on a basketball, then spinning it. Despite
the spinning, the point under your finger hasn't moved. If the only
qualification you have to meet is to have the original point end up
at a new location, how are you to choose between these different
possible rotations?
A simple solution can be seen in the diagram to the right. Take the
cross product
of your start and end points (unit length vectors
from the centre of the sphere) to form a rotational axis perpendicular
to both of them. Then to find the angle it must be rotated about
this axis, take their
dot product,
which gives you the
cosine
of that angle.
Calculating the Rotation Matrix
At this point you could just call glRotate knowing the
axis of rotation and getting the angle with an arccosine function,
but you can also keep track of it yourself.
The way to do this is with a special kind of mathematical
construction called a
quaternion.
A quaternion is an extension of two dimensional
complex numbers
to four dimensions (there is no corresponding three dimensional type of number,
interestingly). Specifically for rotations, though, we can think of our
quaternion as a 4D vector (x,y,z,w) where
(x,y,z) would point along our rotational axis in 3D,
and w is related to our angle.
(There is a good description of using quaternions for rotation at
Genesis 3D.)
If we have a unit vector (x,y,z), we may obtain
the correct magnitude of the quaternion's (x,y,z) by
multiplying them by the sine of half the angle of rotation.
Finally w is determined to be the cosine of half the
angle rotation. Once known, all of these values can be assembled into a
rotation matrix that looks like the following:
| w2 + x2 - y2 - z2 |
2xy + 2wz |
2xz - 2wy |
0 |
| 2xy - 2wz |
w2 - x2 + y2 - z2 |
2yz + 2wx |
0 |
| 2xz + 2wy |
2yz - 2wx |
w2 - x2 - y2 + z2 |
0 |
| 0 |
0 |
0 |
w2 + x2 + y2 + z2 |
The generation of this matrix can be slightly simplified knowing that
(w2 + x2 + y2 + z2) = 1.
If this sum is not equal to 1, the corresponding matrix transformation will
actually cause some sort of scaling as well as the rotation, which would
generally be quite undesirable. (This is why it is important that your
axis of rotation be a unit vector scaled by the sine of
the half angle. They combine with its cosine to form
a 4D vector that is also of unit length.)
Once you have your rotation matrix, however, you can multiply it by
whatever matrix you were using when the starting vector was gathered,
and pass the result to glMultMatrix, which will apply the
transformation for you.
That's it! There is much more that can be said about quaternions,
but that is a big topic and not directly related to the arcball. Take
a look at the source code in the ZIP file for clues as to how to
implement the thing, but as always if you have questions, send me
an e-mail.
brad

rainwarrior.ca
2008-5-5

